다음과 같은 행렬들을 곱한다고 해보자.
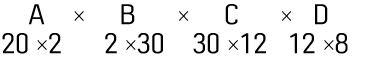
괄호를 어떻게 치든지 결과값은 모두 같을 것이다. 하지만 괄호에 따라서 곱셈 연산의 수는 모두 상이하다. 요런 식으로.

위의 그림에 보이듯이 곱셈 연산의 수가 엄청나게 차이가 난다. 그럼 더 적은 곱셈 연산으로 행렬을 곱하기 위해선 어떻게 해야 할까?
이에 대한 문제가 바로 연쇄 행렬 곱셈 (Chained Matrix Multiplication) 문제이다.
이 연쇄 행렬 곱셈 문제는 다이나믹 프로그래밍을 통해 구할 수 있다. optimal 한 부분 수열을 이용하는 것이다.
- 전체 행렬에 있어서, 두 개의 부분 수열로 분리한다.
- 각 부분 수열에 있어서, 최소 비용을 구한 후 합쳐준다
- 이 과정을 분리할 수 있을 때까지 부분 수열의 길이를 늘려주면서 반복한다.
사용되는 변수는 다음과 같다.

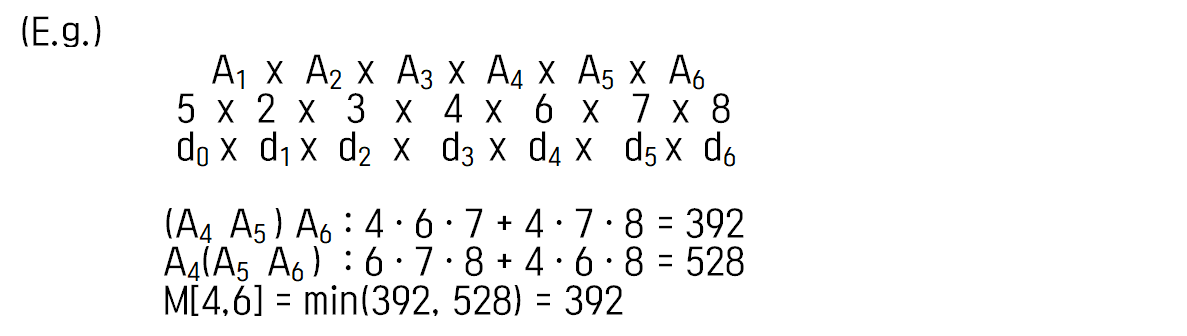
이런 식으로 해보면 다음과 같은 점화식을 구할 수 있다.

따라서 M[1, 2] 부터 M[N-1, N]을 구하고, M[1, 3] 부터 M[N-2, N] ... 이런 식으로 2차원 배열 M에 대해 오른쪽 방향으로 대각선을 채워나가면서 궁극적으로 M[1, N]을 구하면 되는 것이다.
아래는 수도 코드이다.
Function minmult(n:integer; d: array[0…n] of integer;
var p: array[1…n-1,1..n] of index): integer;
var i,j,k,diagonal: index;
M : array[1..n,1..n] of integer;
{ For i=1 to n do M[i,i]=0;
For diagonal =1 to n-1 do
For i=1 to n-diagonal do {
j=i+diagonal;
M[i,j]=
p[i.j]=a value of such k; }
minmult =M[1,n];
}수도 코드만 보고는 이해하기 어려울 수 있으니 여기를 참고하면 좋겠당. ㅎ
가장 기본적인 문제인 백준 사이트의 행렬 곱셈 순서라는 문제 풀이 글이다..ㅎ
Reference
경북대학교 컴퓨터학부 유관우 교수님 강의 자료
https://mygumi.tistory.com/258
'Algorithm > 알고리즘' 카테고리의 다른 글
| 위상 정렬(Topological Sort) (0) | 2020.09.24 |
|---|---|
| [SSSP(1)] Dijkstra Algorithm (2) | 2020.09.01 |
| 정렬(Sorting) (0) | 2020.06.15 |
| 유클리드 호제법(Euclidean Algorithm) (6) | 2020.06.15 |


