Path with Maximum Probability - LeetCode
Can you solve this real interview question? Path with Maximum Probability - You are given an undirected weighted graph of n nodes (0-indexed), represented by an edge list where edges[i] = [a, b] is an undirected edge connecting the nodes a and b wi
leetcode.com
오랜만에 미듐 문제를 건드려 보았습니다. 우째 푸는지 몰라서 멋쟁이 형님의 유튭 강의를 보고 풀었습니다.^^~
요 문제.. 재밌네용. 오랜만에 다익스트라 알고리즘을 끄적여봤습니다.
다만 이 문제에서는 최단 경로가 아닌, 가장 높은 확률을 가지는 루트의 확률을 구해야 합니다. 따라서 최대 힙(Max Heap) 을 사용해야겠지요.
class Solution {
private static class Node implements Comparable<Node> {
private int to;
private double prob;
public Node(int to, double prob) {
this.to = to;
this.prob = prob;
}
public int compareTo(Node obj) {
if (this.prob < obj.prob) return 1;
else if (this.prob == obj.prob) return 0;
else return -1;
}
}
public double maxProbability(int n, int[][] edges, double[] succProb, int start, int end) {
double answer = 0.0;
PriorityQueue<Node> maxHeap = new PriorityQueue<>();
Map<Integer, List<Node>> graph = makeGraph(edges, succProb);
boolean[] v = new boolean[n];
maxHeap.add(new Node(start, 1.0));
while (!maxHeap.isEmpty()) {
Node cur = maxHeap.poll();
v[cur.to] = true;
if (cur.to == end) {
answer = cur.prob;
break;
}
if (!graph.containsKey(cur.to)) continue;
for (Node next : graph.get(cur.to)) {
if (v[next.to]) continue;
maxHeap.add(new Node(next.to, next.prob * cur.prob));
}
}
return answer;
}
private Map<Integer, List<Node>> makeGraph(int[][] edges, double[] prob) {
Map<Integer, List<Node>> graph = new HashMap<>();
for (int i = 0; i < edges.length; i++) {
int[] edge = edges[i];
insertNode(graph, edge[0], edge[1], prob[i]);
insertNode(graph, edge[1], edge[0], prob[i]);
}
return graph;
}
private void insertNode(Map<Integer, List<Node>> graph, int from, int to, double prob) {
List<Node> temp = graph.getOrDefault(from, new ArrayList<>());
temp.add(new Node(to, prob));
graph.put(from, temp);
}
}
쬐끔 깁니다.
먼저 최대 힙과 그래프를 구성할 Node 클래스를 선언해줍니다. 필드 변수로는 경로의 성공 확률(subProb), 그리고 to 는
- 그래프에서는 가야할 다음 노드,
- 최대 힙에서는 현재 노드
가 되겠습니다. 변수명이 쪼끔 맘에 안들긴 하지만 넘어갑쉬다~ 저는 개인적으로 맵 - 리스트로 그래프를 표현하는 걸 선호해서 to 로 지었습니다.
방향이 없는 그래프니 양방향으로 그래프를 구성해주고.. 이제 다익스트라 알고리즘을 써먹을 차례입니다.
우선순위 큐를 사용하면 너무 쉽져. 시작점을 넣어주고 마구마구 반복문을 굴려줍니다. 최대 힙에서 한 놈을 빼서 이웃한 노드들의 가중치(성공 확률)을 보면서 재계산해서 최대 힙에 다시 넣어주면 됩니다. 성공 확률은 지금 현재 노드까지 경로의 성공 확률 * 다음 노드로의 경로의 성공 확률 입니다. (maxHeap.add(new Node(next.to, next.prob * cur.prob)))
그래서 정답은 어떻게 구하냐면~~
최대 힙을 구성하고 있기 때문에 최대 힙에서 뺀 노드가 도착 노드와 같다면 그때의 성공 확률이 바로 정답이 됩니다.
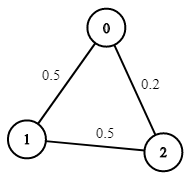
얘로 예시를 들어 보면..
먼저 최대 힙에 시작점 {to: 0, prob: 1.0} 을 넣고 시작합니다. 가중치는 곱해야 하므로 초기값은 1.0입니당.
그럼 시작점의 이웃들을 최대 힙에 또 넣습니다. {to: 1, prob: 0.5}, {to: 2, prob: 0.2}
이 다음 뽑힐 친구는 {to: 1, prob: 0.5} 가 되겠죠. 성공 확률이 더 높으니까요.
다시 얘 친구들을 봅시다. 노드 0은 이미 방문을 했고.. {to: 2, prob: 0.5 * 0.5} 를 넣어줍니다.
그럼 이제 최대 힙에는 {to: 2, prob: 0.2} 와 {to: 2, prob: 0.25} 가 남았는데요, 여기서는 성공 확률이 0.25 인 {to: 2, prob: 0.25} 가 뽑힙니다.
이제 도착점에 도착했으니 정답은 바로 0.25가 되는 것이지요~~
이지 문제말고 쫌 더 머릴 쓰는 문제를 풀어야 훈련이 될텐데.. 퇴근하고 나면 머리 쓰는 문제 푸는게 너무너무 힘드네요...
그래도 화이팅~!~!
감사합니다~!!!
'Algorithm > LeetCode' 카테고리의 다른 글
| [Prefix Sum(Product)] 238. Product of Array Except Self (0) | 2024.03.15 |
|---|---|
| [Greedy/우선순위 큐] 1642. Furthest Building You Can Reach (0) | 2024.02.26 |
| [배열/시뮬레이션] 59. Spiral Matrix II (0) | 2023.05.10 |
| [배열/시뮬레이션] 54. Spiral Matrix (0) | 2023.05.10 |
| [DP] 64. Minimum Path Sum - Java (0) | 2023.03.27 |